EMアルゴリズム(Expectation-Maximization Algorithm)
確率モデルが観測できない変数(潜在変数/隠れ変数)に依存する場合に最尤法を実施するためのアルゴリズム。非常に多くの応用に使え、変分ベイズ法などの基礎を成すのでとっても大事なアルゴリズム。
推定の流れ
このアルゴリズムでは、現在のパラメータ( )と観測変数(
)と観測変数( )から得られる情報を使って、潜在変数(
)から得られる情報を使って、潜在変数( )の条件付き確率(
)の条件付き確率( )を求めるステップ(E-Step)と、観測変数の事後確率の期待値を最大化するフェーズ(M-Step)の二段階の処理を繰り返しながらパラメータを最適化する。
)を求めるステップ(E-Step)と、観測変数の事後確率の期待値を最大化するフェーズ(M-Step)の二段階の処理を繰り返しながらパラメータを最適化する。
つまり、尤度関数( )の最大化を一発で計算したいところなのだが、それは難しいので、今の
)の最大化を一発で計算したいところなのだが、それは難しいので、今の を使って計算される
を使って計算される を利用して、尤度関数の期待値(
を利用して、尤度関数の期待値( )の最大化という問題に置き換えている。実際には、最後の式を2つ目の
)の最大化という問題に置き換えている。実際には、最後の式を2つ目の を構成する各変数について偏微分して0になる値を探すなどを行って更新することになる。
を構成する各変数について偏微分して0になる値を探すなどを行って更新することになる。
つまり、尤度関数(
詳細な定式化(間違ってるかも)
パラメータを 、観測変数を
、観測変数を 、潜在変数を
、潜在変数を とする。
とする。
目的は、観測変数のパラメータに対する確率 の最大化。ところが、潜在変数があるので
の最大化。ところが、潜在変数があるので の周辺化で置き換えて話を進められるようにする。そこでベイズの公式による式変形を行う。
の周辺化で置き換えて話を進められるようにする。そこでベイズの公式による式変形を行う。
目的は、観測変数のパラメータに対する確率
さて、ここで天下りながら分布 を導入する。これは潜在変数
を導入する。これは潜在変数 の事後分布の近似分布である。式変形のミソは、この分布
の事後分布の近似分布である。式変形のミソは、この分布 と
と の間の違い(距離)が現れるように前式を変形していくことである。そこで、まず右辺の分子分母を
の間の違い(距離)が現れるように前式を変形していくことである。そこで、まず右辺の分子分母を で割る。
で割る。
次に両辺に対数をとる。
さらに両辺に をかけて
をかけて に関し周辺化を行う。
に関し周辺化を行う。
左辺において、 は
は に関係せず、
に関係せず、 は1となる。
は1となる。
右辺の第一項を 、第二項を
、第二項を とかくと、下記式を得ることができる。
とかくと、下記式を得ることができる。
右辺の第一項を
この式において最適化で変更できるのは と
と である。EMアルゴリズムは、この2つの視点で交互に最大化する。
である。EMアルゴリズムは、この2つの視点で交互に最大化する。
まずEステップでは、 は0以上なので、
は0以上なので、 を最小化することで
を最小化することで を最大化する。KL距離の定義より
を最大化する。KL距離の定義より は
は のとき最小化となる。すなわち、
のとき最小化となる。すなわち、 を固定し
を固定し に
に を設定すればよい。
を設定すればよい。
まずEステップでは、
次いでMステップでは、 を固定し
を固定し に関して最大化する。すなわち、下記式を
に関して最大化する。すなわち、下記式を に関して最大化する。ここで、Eステップ時点で利用した
に関して最大化する。ここで、Eステップ時点で利用した の値は、
の値は、 として固定されている。
として固定されている。
上述において、 は
は の下界をなしており、Eステップではこの下界を最大化する
の下界をなしており、Eステップではこの下界を最大化する を手に入れている。一方、Mステップでは、
を手に入れている。一方、Mステップでは、 が
が に関して最大化されるわけだが、このとき新しい
に関して最大化されるわけだが、このとき新しい を使った
を使った と今までの
と今までの との間に新たな違い(距離)が生まれる。そのため、EステップとMステップを繰り返すことで徐々に
との間に新たな違い(距離)が生まれる。そのため、EステップとMステップを繰り返すことで徐々に を最大化していく必要がある。
を最大化していく必要がある。
実装例
言語
Python 2.6 + scipy + matplotlib
問題設定
2つの正規分布からなる2次元の混合正規分布に対して平均、分散、負担率を推定する。
詳細はソース参照。
詳細はソース参照。
ソース
結果
- コンソール最後の部分
<< 29 >>
[ 0 ]
Mu=
[[ 21.05175707]
[ 21.65353366]]
Sigma=
[[ 95.11897414 9.67571604]
[ 9.67571604 116.52378045]]
Pi=
0.674809728052
[ 1 ]
Mu=
[[-14.92553657]
[-10.79587385]]
Sigma=
[[ 137.40967457 -2.5813963 ]
[ -2.5813963 95.53296063]]
Pi=
0.325190271948
- グラフ
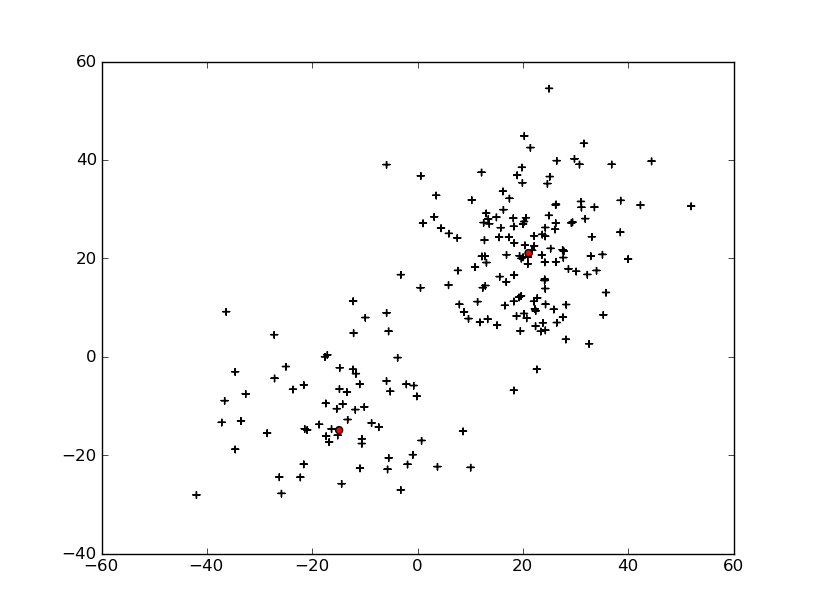
補足
この例ではうまくいくが、もとの正規分布の分散が大きすぎると一つの正規分布でほとんどのデータを説明し、もう一つの正規分布がごくわずか(1点)のデータを説明しようとしてしまう。このあたりは、分散の監視などが必要。
また、そもそもの収束判定には尤度関数の値の変化率を見るのが一般的。
また、そもそもの収束判定には尤度関数の値の変化率を見るのが一般的。
添付ファイル
