一次変調信号を拡散させた信号を伝送する際に、最適にRCCフィルタを設定しなければならない。
指定された帯域内で信号を送信するため、パルス整形フィルタでデータビットが成形される。
その信号はキャリア変調部と無線周波数(RF)変換部を通過してアンテナを通して空気中に送信される。
(参考資料:
altera,
fujitsu,
慶応)
W-CDMAではチャネライゼーションとスクランブルという拡散が行われており、
前者が同セル内でユーザ間を識別したり、マルチコード伝送(1ユーザが複数チャネルを使うこと?)を実現するのに使われている。
後者はセル間の識別に用いられている。
一般的にはチャネライゼーションに直行符号、スクランブルにGold符号が用いられている。
alteraの仕様書ではどちらの拡散もQPSK変調する前に行っている。
一方fujitsuの仕様書ではチャネライゼーションをQPSK変調前に、スクランブルをその後に行っている。
この参考ではScrambleした後にナイキストフィルタにかけて送信している。
ナイキストフィルタ
T秒ごとに標本化された標本(ディジタル信号)をフィルタを通したとき、出力波形のT秒ごとの標本値が元の値と完全に等しくなるようなLPFをナイキストフィルタという。
パラメータはサンプリング周波数fsで1/2fsに帯域を制限することができる。
BPSKはマッピングと帯域制限のコンポーネントで構成されていて、入力ビットに対して複素信号を出力する。
参考
以下神谷先生著 MATLABによるディジタル無線信号処理技術一部抜粋
実際のフィルタ出力はそれぞれのSinc関数波形の和となることに注意する。
このように得られた出力の帯域幅は、通信路の帯域幅と同じに制限されることになるので、この信号の電力はすべて通信路を通過でき、
波形の歪みは生じない。
ここで重要なことは、それぞれのSinc関数波形の頂点において、他のインパルスで生じたSinc関数波形は0となっていることである。
したがって、受信機においてSinc関数の中心の値をサンプリングすることによって符号間干渉を避けることができる。
このことから、ナイキストフィルタを用いることによって、0Hzを中心として両側f0までの帯域では、t=0.5f0の間隔で符号間干渉なくインパルスを送信できる。
インパルスがディジタル変調のシンボルであることを考えると、シンボルレートは2f0spsとなる。
RRCフィルタ
よく使われるナイキストフィルタの一つ。
dbpsk.pyでは以下のように使っている。
# pulse shaping filter
ntaps = 11 * self._samples_per_symbol //22タップ数分(sps=2の場合)、一度のフィルタ出力に影響を与える。
self.rrc_taps = gr.firdes.root_raised_cosine(
self._samples_per_symbol, # gain (samples_per_symbol since we're
# interpolating by samples_per_symbol)
self._samples_per_symbol, # sampling rate ここの値はbenchmarkではよく2になっている!
1.0, # symbol rate
self._excess_bw, # excess bandwidth (roll-off factor)
ntaps)
self.rrc_filter = gr.interp_fir_filter_ccf(self._samples_per_symbol,
self.rrc_taps)
サンプリングレート及びシンボルレートを引数に指定するが、これは1シンボル(bpskの場合ビット)送るのに何サンプルを使うかを
求めたいだけだから、ディジタルフィルタの場合、上に示すようにして引数を指定してもよい。第2引数は作成したフィルタタップを指定
以下、gr_firdes.h及びccの定義(RCCフィルタタップの作成)
/*!
* \brief design a Root Cosine FIR Filter (do we need a window?)
*
* \p gain: overall gain of filter (typically 1.0)
* \p sampling_freq: sampling freq (Hz)
* \p symbol rate: symbol rate, must be a factor of sample rate
* \p alpha: excess bandwidth factor
* \p ntaps: number of taps
*/
static std::vector<float>
root_raised_cosine (double gain,
double sampling_freq,
double symbol_rate, // Symbol rate, NOT bitrate (unless BPSK)
double alpha, // Excess Bandwidth Factor
int ntaps);
vector<float>
gr_firdes::root_raised_cosine (double gain,
double sampling_freq,
double symbol_rate,
double alpha,
int ntaps)
{
ntaps |= 1; // ensure that ntaps is odd
double spb = sampling_freq/symbol_rate; // samples per bit/symbol 1シンボル(bpskの場合ビット)送るのに何サンプルを使うか。(spb = 1)
//シンボルレートは最大でサンプリング周波数の半分だけ送れる。なのにどっちも2で大丈夫なのだろうか?→間違い!
//シンボルレートは最大でサンプリング分だけ送れる。シンボルレートは周波数ではない!単位が(Hz)ではない。bar / sec
//シンボルレート=サンプリング周波数は間引かないということ?これを離散時間で考えるとどういうことなんだろう?
//多分一つのsinc波形と22個分の入力の相互相関係数を出力する!(最終的にインストールされるのは11個分のフィルタ二つだから1周期分の相関)
vector<float> taps(ntaps);
double scale = 0;
for(int i=0;i<ntaps;i++) //全タップ数22
{
double x1,x2,x3,num,den;
double xindx = i - ntaps/2; //-10から10の整数値
x1 = M_PI * xindx/spb; //常に2π×n
x2 = 4 * alpha * xindx / spb; //-10から10倍
x3 = x2*x2 - 1; //99から-1から99
if( fabs(x3) >= 0.000001 ) // Avoid Rounding errors...
{
if( i != ntaps/2 )
num = cos((1+alpha)*x1) + sin((1-alpha)*x1)/(4*alpha*xindx/spb);
else
num = cos((1+alpha)*x1) + (1-alpha) * M_PI / (4*alpha);
den = x3 * M_PI;
}
else
{
if(alpha==1)
{
taps[i] = -1;
continue;
}
x3 = (1-alpha)*x1;
x2 = (1+alpha)*x1;
num = (sin(x2)*(1+alpha)*M_PI
- cos(x3)*((1-alpha)*M_PI*spb)/(4*alpha*xindx)
+ sin(x3)*spb*spb/(4*alpha*xindx*xindx)); //この辺でSinc関数っぽくなっている。(denで割ると)
den = -32 * M_PI * alpha * alpha * xindx/spb;
}
taps[i] = 4 * alpha * num / den;
scale += taps[i];
}
for(int i=0;i<ntaps;i++)
taps[i] = taps[i] * gain / scale; //正規化してタップ完成
return taps;
}
LPFの実装(gr_interp_fir_filter_ccf.cc)
//コンストラクタ。第一引数に1サンプルをいくつに増やすか決めている。
gr_interp_fir_filter_ccf::gr_interp_fir_filter_ccf (unsigned interpolation, const std::vector<float> &taps)
: gr_sync_interpolator ("interp_fir_filter_ccf",
gr_make_io_signature (1, 1, sizeof (gr_complex)),
gr_make_io_signature (1, 1, sizeof (gr_complex)),
interpolation),
d_updated (false), d_firs (interpolation)
{
if (interpolation == 0)
throw std::out_of_range ("interpolation must be > 0");
std::vector<float> dummy_taps;
for (unsigned i = 0; i < interpolation; i++)
d_firs[i] = gr_fir_util::create_gr_fir_ccf (dummy_taps);
set_taps (taps); //タップをセット
install_taps(d_new_taps);
}
//ワーク
int
gr_interp_fir_filter_ccf::work (int noutput_items,
gr_vector_const_void_star &input_items,
gr_vector_void_star &output_items)
{
const gr_complex *in = (const gr_complex *) input_items[0];
gr_complex *out = (gr_complex *) output_items[0];
if (d_updated) {
install_taps (d_new_taps);
return 0; // history requirements may have changed.
}
int nfilters = interpolation (); //2(samples/symbol)
int ni = noutput_items / interpolation (); //22/2=11:補間を除いたタップすう。
for (int i = 0; i < ni; i++){ //11
for (int nf = 0; nf < nfilters; nf++) //2
out[nf] = d_firs[nf]->filter (&in[i]); //微妙に値の異なる値をかけてる。nfilters = samples/symbolsだからこの値が大きいほどなめらかになる。
/*!
* \brief compute a single output value.
*
* \p input must have ntaps() valid entries.
* input[0] .. input[ntaps() - 1] are referenced to compute the output value.
*
* \returns the filtered input value.
*/
//virtual gr_complex filter (const gr_complex input[]) = 0;
out += nfilters;
}
return noutput_items;
}
//タップをセット!
void
gr_interp_fir_filter_ccf::set_taps (const std::vector<float> &taps)
{
d_new_taps = taps;
d_updated = true;
// round up length to a multiple of the interpolation factor
int n = taps.size () % interpolation ();
if (n > 0){
n = interpolation () - n;
while (n-- > 0)
d_new_taps.insert(d_new_taps.begin(), 0);
}
assert (d_new_taps.size () % interpolation () == 0);//なぜ補間数で割りきれるとエラーがでるのか??分からん。。→いやこれが偽の場合assert!!
}
//d_fir(2次元)にtapsをインストール
void
gr_interp_fir_filter_ccf::install_taps (const std::vector<float> &taps)
{
int nfilters = interpolation (); //2(samples / symbol)だとする。
int nt = taps.size () / nfilters; //補間を除いたタップ数11(=22/2:default)。
assert (nt * nfilters == (int) taps.size ()); //11*2=22
std::vector< std::vector <float> > xtaps (nfilters); //vectorのアドレスを入れる。
for (int n = 0; n < nfilters; n++)
xtaps[n].resize (nt); //22個から11個の配列にresizeする。
for (int i = 0; i < (int) taps.size(); i++)
xtaps[i % nfilters][i / nfilters] = taps[i]; //taps[i]を順番にxtaps(i,0)とxtaps(i+1,1)にどんどん入れてく。(つまり、補完を取り除いたタップが一列に並ぶ)
for (int n = 0; n < nfilters; n++)
d_firs[n]->set_taps (xtaps[n]); //補間を取り除いたタップをd_firs(二次元配列)にセット。
set_history (nt); //11個をヒストリーにセットする。
d_updated = false;
#if 0
for (int i = 0; i < nfilters; i++){
std::cout << "filter[" << i << "] = "; //
for (int j = 0; j < nt; j++)
std::cout << xtaps[i][j] << " ";
std::cout << "\n";
}
#endif
}
受信側でも送信側でも同じ数のタップ数を作る。
送信側は一つの入力を二回、別々のタップに適用する。
一方、受信側は一つの入力を一回だけあるタップに適用する。
これは既に入力はsample_per_symbol倍されているから。
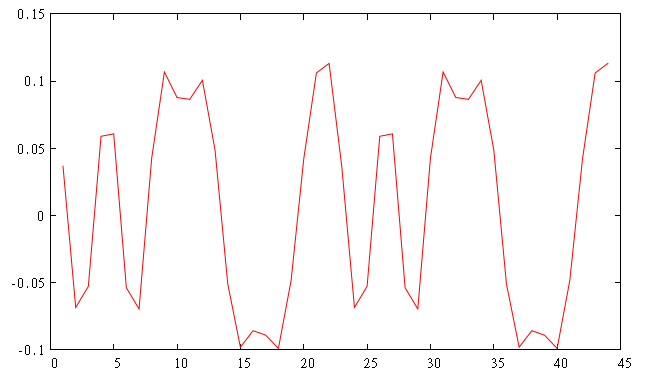
送信側ナイキスト波形
受信側ナイキスト波形
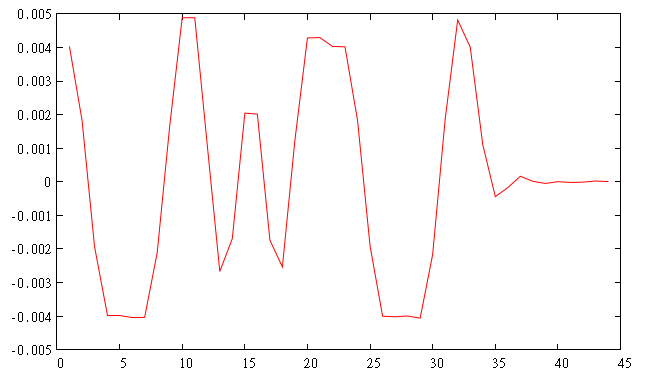
図の例では11個の信号をリピートして送っている。(samples_per_symbol=2)
signal = {1, -1 ,-1 ,-1, 1, 1, -1, 1, -1, 1, 1}
最終更新:2011年07月19日 20:57

