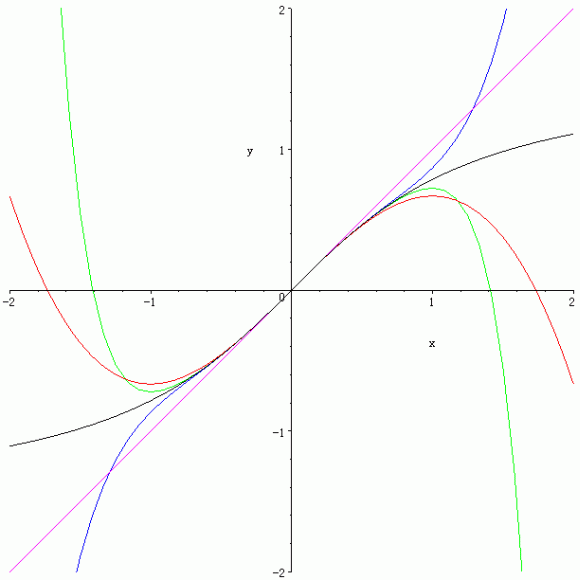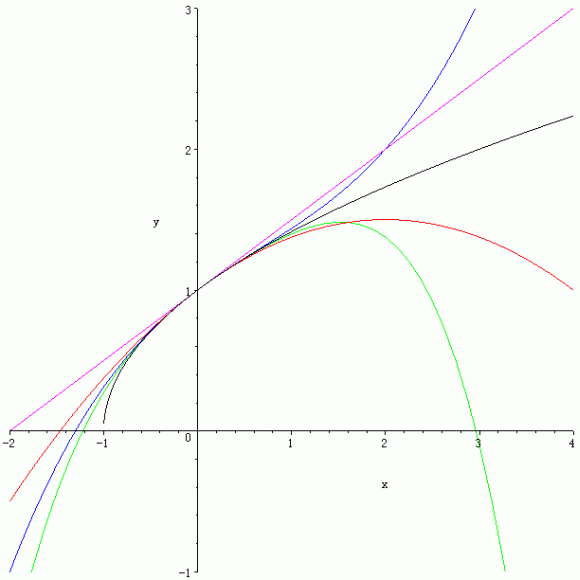目次
y = arctan x の x=0 におけるTaylor展開の状況
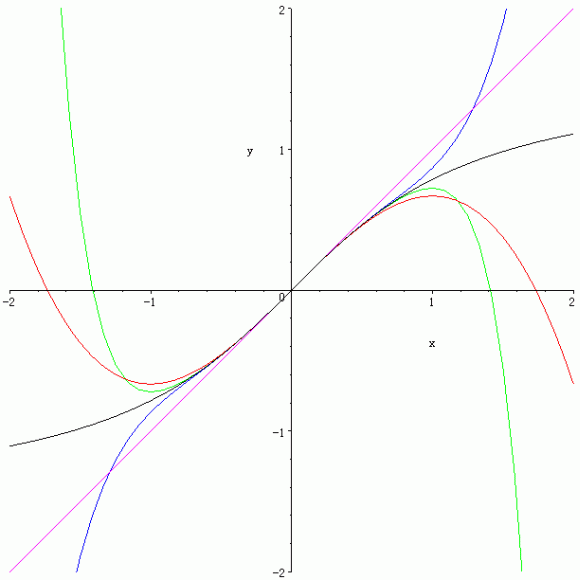
y = arctan x (黒), y = x (紫), y = x - x3/3 (赤), y = x - x3/3 + x5/5(青), y = x - x3/3 + x5/5 - x7/7(緑).
y = ex の x=0 におけるTaylor展開の状況
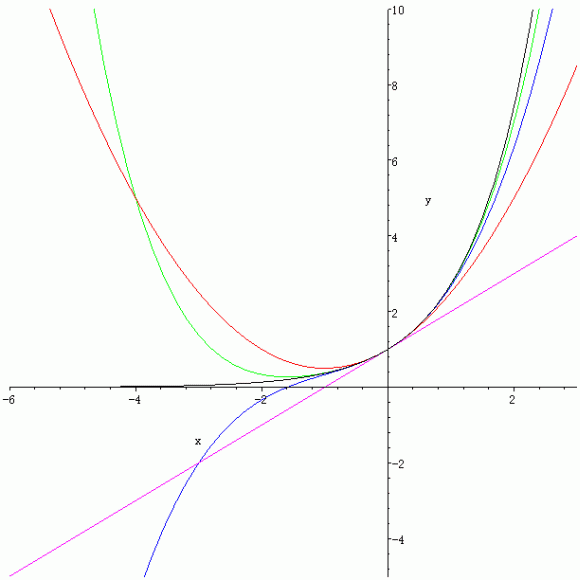
y = ex (黒), y = 1 + x (紫), y = 1 + x + x2/2 (赤), y = 1 + x + x2/2 + x3/6(青), y = 1 + x + x2/2 + x3/6 + x4/24(緑).
y = sin x の x=0 におけるTaylor展開の状況
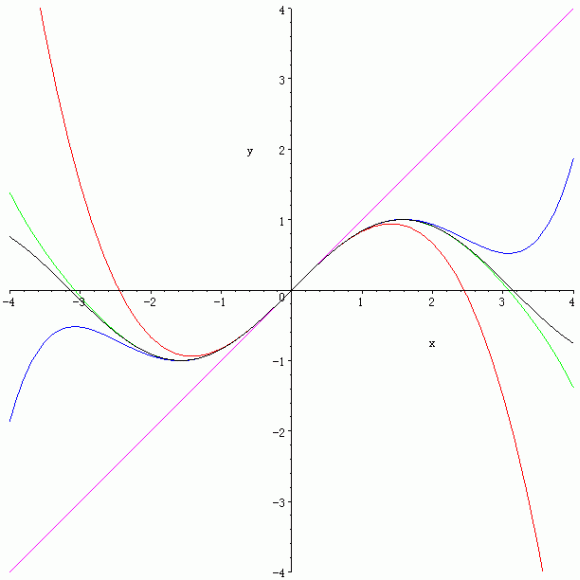
y = sin x (黒), y = x (紫), y = x - x3/6 (赤), y = x - x3/6 + x5/120(青), y = x - x3/6 + x5/120 - x7/5040(緑).
y = cos x の x=0 におけるTaylor展開の状況
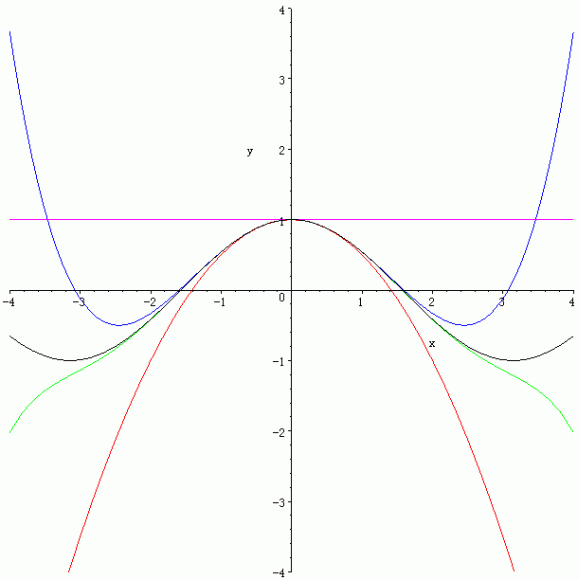
y = cos x (黒), y = 1 (紫), y = 1 - x2/2 (赤), y = 1 - x2/2 + x4/24 (青), y = 1 - x2/2 + x4/24 - x6/720 (緑).
y = (1+x)1/2 の x=0 におけるTaylor展開の状況
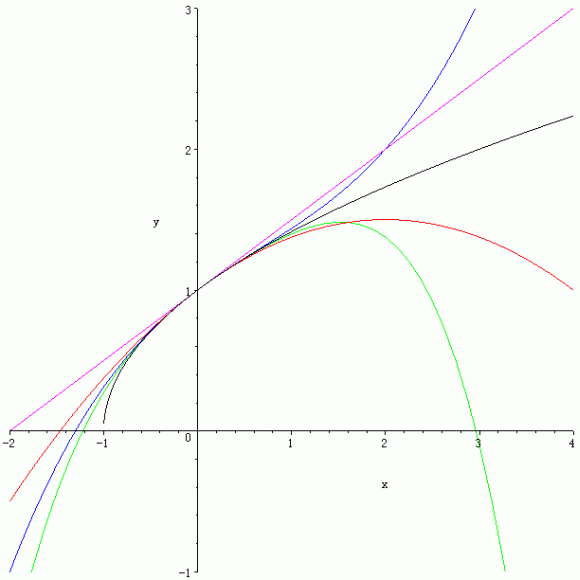
y = (1+x)1/2 (黒), y = 1 + x/2 (紫), y = 1 + x/2 - x2/8 (赤), y = 1 + x/2 - x2/8 + x3/16(青), y = 1 + x/2 - x2/8 + x3/16 - 5x4/128(緑).
y = log x の x=1 におけるTaylor展開の状況
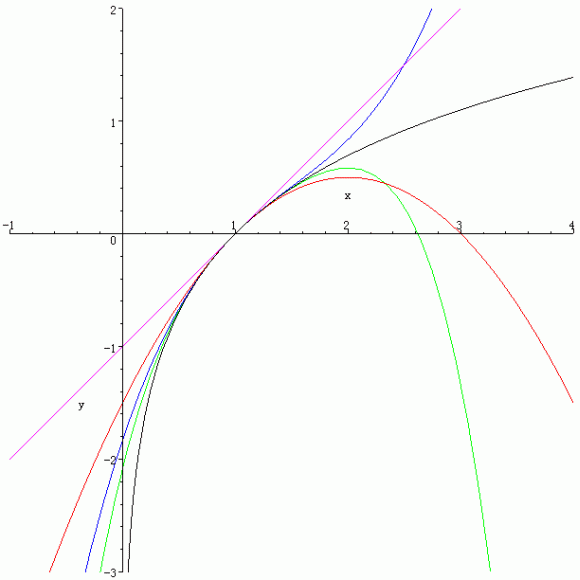
y = log x (黒), y = x-1 (紫), y = (x-1) - (x-1)2/2 (赤), y = (x-1) - (x-1)2/2 + (x-1)3/3 (青), y = (x-1) - (x-1)2/2 + (x-1)3/3 - (x-1)4/4 (緑).
最終更新:2010年06月01日 11:00