デジクリwiki

アルゴリズム講座―台形近似積分

コンピュータに積分をさせるとなると、(積分公式は使えないので)やはり近似的な方法を使うことになります。代表的な方法として

長方形近似法
台形近似法
シンプソン法

という方法が知られています。ここでは、台形近似による積分を扱います。

まず根本的に、どういう風に処理させるかを考えます。これは、非常に積分にとって原始的な方法をとることになります。すなわち、グラフを非常に小さく区切り、それぞれの区切られた区間の面積を求めていくことで実現します。以下の赤い部分ようなイメージです。

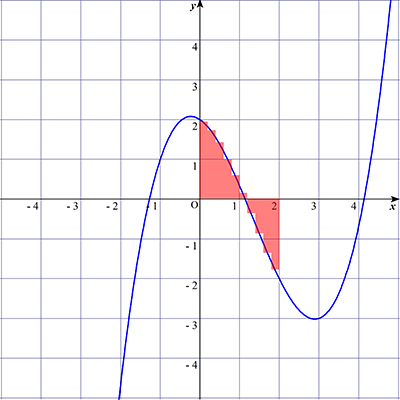
台形近似法では、これを台形に見立てて、その面積を足していく方針で積分を行います。

では、台形積分をする関数trap_integ(double (*func)(double a),double low,double high,double h)です。

仕様
機能:渡されたポインタの関数について、与えられた区間内で台形近似による積分を行います。
引数:double (*func)(double a)…引数にdouble型を一つ、返値がdouble型の、積分を行う関数へのポインタ
 　　low…積分を行う区間の最低値
 　　high…積分を行う区間の最高値
 　　h…台形の高さをhにして計算します
返値:積分をした計算結果を返します

double integ(double (*func)(double a),double low,double high,double h){
	double x,result;
	for(x=low;x<=high;x+=h){
		result+=((*func)(x+h)+(*func)(x))*h/2;
	}
	return result;
}

使用例です。ここでは、f(x)=3x^2の0～2の区間について積分を行います。上の関数と一緒に書いて実行してみてください(ちなみに理論値は8、h=0.00001くらいにすると結果も8.000000になる)。

#include <stdio.h>

double function(double);

int main(void){
	printf("%lf\n",integ(function,0,2,0.001));
}

double function(double x){
	return 3*x*x;
}